Logistic Regression in Machine Learning
Logistic regression is a function that translates input into one of the two categories (a binomial classifier).
You can think of logistic regression as an on-off switch. It can stand alone, or some version of it may be used as a mathematical component to form switches, or gates, that relay or block the flow of information.
Like any switch, logistic regression can be a component in a larger circuit. It is the transistor of machine learning. Instead of regulating current, or voltage flow, in a circuit board, logistic regression regulates the signal flowing from input data through a larger algorithm to the predictions that it makes.
On a circuit board, a transistor might receive voltage that opens a current to turn on a light. In a machine-learning algorithm, logistic regression allows signal through, or not, to make a classification.
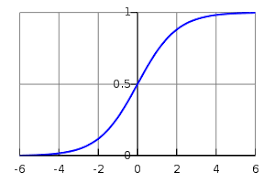
The image above traces a logistic function. As you can see, it is s-shaped, or sigmoid, flattening out at the top and bottom, while transitioning quickly between the two states before entering one of the long, asymptotic tails. What that means is, the input can build up for a long time while still being interpreted by the function as “off”, but by adding incrementally more signal at just the right place, the function flips to “on”, and it remains “on” forever.
Logistic regression is widely used in statistics, and it was originally applied in ecology to the study of populations, whose growth tends to plateau as they exhaust the resources at their disposal.1
As a function, logistic regression is simply an S-shaped curve that can ingest any real-valued number, and translate it to a value between 0 and 1. In the graph above, we take continuous values between -6 and 6 and map them to values between 0 and 1. Here is the formula that performs that mapping:
![]()
‘e’ is a mathematical constant known as Euler’s number, an irrational number that is approximately 2.71828. It is the base of the natural logarithms (which answer the question: which number x when multiplied by itself, produces number y. Logarithms look like a flattening hill, while exponential functions, their inverses, look like a mountain being beamed up to a spaceship).
In this same formula, z is the sum of all inputs that are being used to make a prediction; i.e. z = b0 + b1 + b2 + b3.