Regularization in Machine Learning
For any machine learning problem, essentially, you can break your data points into two components — pattern + stochastic noise.
For instance, if you were to model the price of an apartment, you know that the price depends on the area of the apartment, no. of bedrooms, etc. So those factors contribute to the pattern — more bedrooms would typically lead to higher prices. However, all apartments with the same area and no. of bedrooms do not have the same price. The variation in price is noise.
As another example, consider driving. Given a curve with a specific curvature, there is an optimal direction of steering and an optimal speed. When you observe 100 drivers on that curve, most of them would be close to that optimal steering angle and speed. But they will not have the same steering angle and speed. So again, the curvature of the road contributes to the pattern for steering angle and speed, and then there are noise-causing deviations from this optimal value.
Now the goal of machine learning is to model the pattern and ignore the noise. Anytime an algorithm is trying to fit the noise in addition to the pattern, it is over fitting.
In the supervised setting, you typically want to match the output of a prediction function to your training labels. So the driving example above, you would want to accurately predict the steering angle and speed. As you keep adding more and more variables — like the curvature of the road, the model of the car, the experience of the driver, weather, mood of the driver, etc. — you tend to make better and better predictions on the training data. However, beyond a point, adding more variables is not helping in modeling the pattern, but only trying to fit the noise. Since the noise is stochastic, this doesn’t generalize well to unseen data, and therefore you have low training error and high test error.
Regularization in Machine Learning: Bias Variance Tradeoff in Linear Regression
Consider the following scenario:
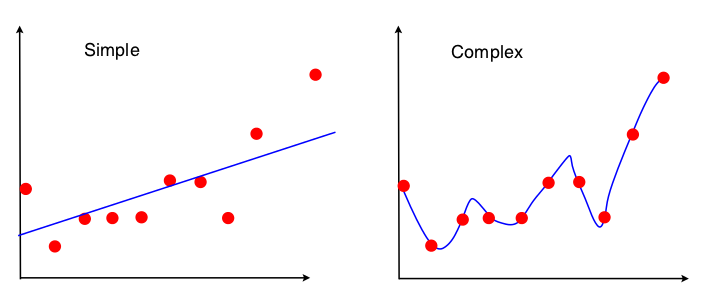
The left algorithm returns the best fit line given those points, while the right algorithm returns the best fit polynomial of degree k given those n points. (k is some large number, like 10, in this example.)
What happens if you move the lowermost point up by some distance?
The line in the left figure becomes slightly flatter — moving a little upwards on the left and remaining at about the same position on the right. The curve on the right, however, changes by quite a bit. The dip that you see between points 1 and 3 might vanish entirely.
The algorithm on the right is fitting the noise. As can be seen from this example, a way to reduce over fitting is then to artificially penalize higher degree polynomials. This ensures that a higher degree polynomial is selected only if it reduces the error significantly compared to a simpler model, to overcome the penalty. This is regularization in Machine Learning.
This technique of adding a "complexity term" to the error term to eliminate very complex functions is called regularization in Machine Learning.
If your model is too flexible, it will not only learn, during training, the general trends that you're interested in, but also the very specific peculiarities that arise in the very specific data samples that you have gathered for training purposes. This is called over-fitting.
Meaning of Regularization in Machine Learning
Regularization is the act of limiting the flexibility of your model so that it will not be able to learn such peculiarities, but will still be powerful enough to learn just the right amount of information.